Towards the Platonic Representation via Multimodal Contrastive Alignment

Introduction

Deep learning models are typically trained to transform raw data into representations optimized for specific tasks. Recently, two lines of research have inspired a deeper inquiry into the nature of these representations. The CLIP framework demonstrated the utility of aligning representations across modalities, using paired image-text data to train joint embeddings for cross-modal retrieval. Meanwhile, the Platonic Representation Hypothesis posits that performant models converge toward a shared statistical model of reality in their representation spaces, suggesting a potential universality underlying learned representations.

This project bridges these ideas by exploring whether representations from disparate pre-trained unimodal neural networks can be aligned into a shared multimodal latent space, inspired by the joint embedding approach of CLIP and motivated by the convergence hypothesis of Platonic Representations. The proposed framework uses frozen unimodal encoders with learned linear adapters to align representations across modalities. Our aim is to determine if such aligned representations better approximate those of larger, more performant models.

Inspired by the success of CLIP in aligning representations across modalities and the theoretical insights of the Platonic Representation Hypothesis, we propose a framework that aligns pre-trained unimodal encoders into a shared multimodal latent space using simple linear adapters. By leveraging frozen encoders such as ResNet-18 for images and DistilBERT for text, we aim to achieve alignment without retraining a larger state-of-the-art model like DINOv2, enabling scalability to new modalities with minimal overhead.

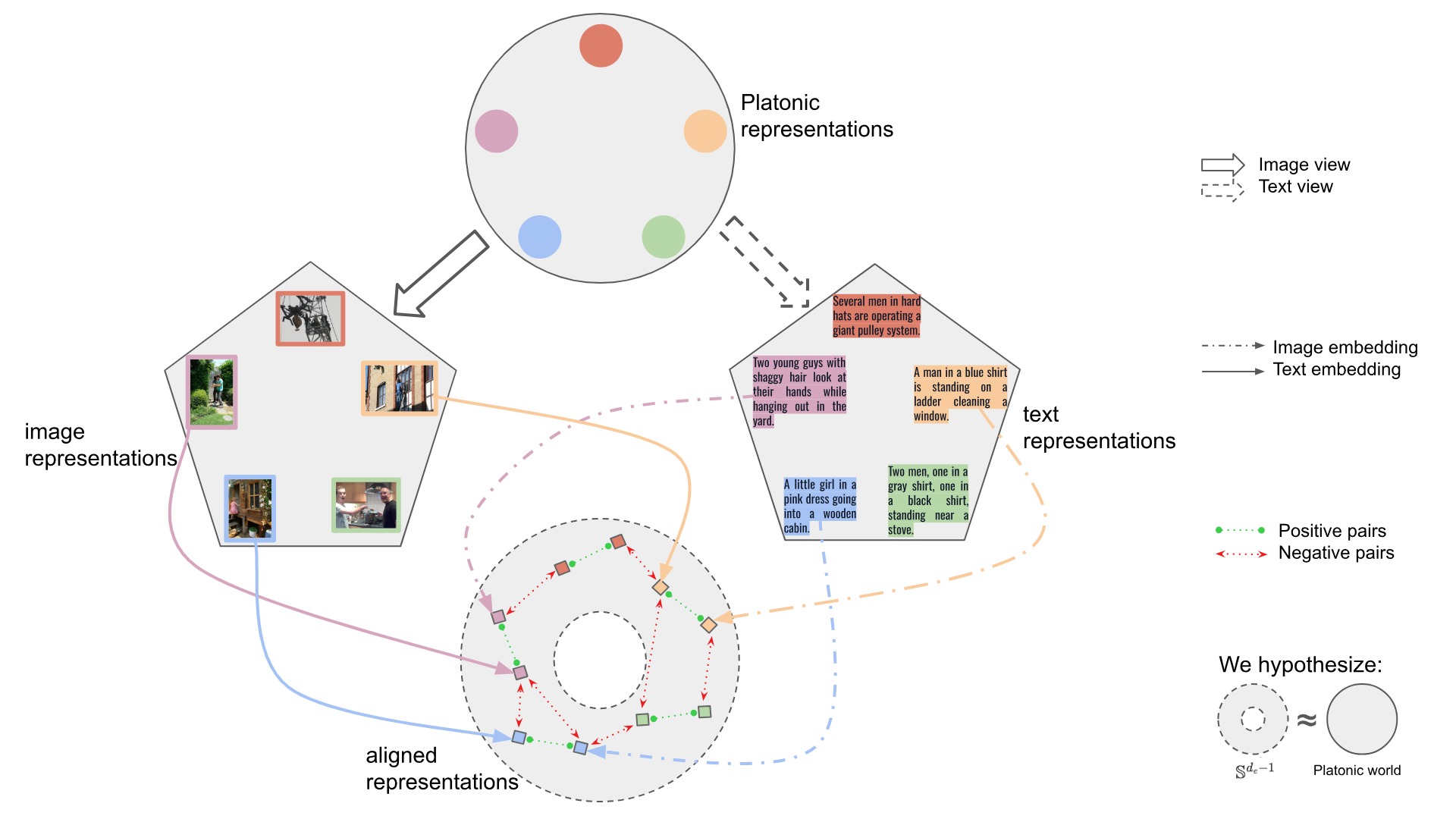Figure 1. Conceptual illustration of our multimodal alignment framework. Representations from ResNet-18 (images) and DistilBERT (text) on the image-caption samples from the Flickr30k dataset are aligned into a shared latent space using lightweight adapters. Matching image-caption pairs are pulled together, while non-matching pairs are pushed apart to create a unified multimodal embedding.

Motivation

Our approach is motivated by three key insights:

1. Inspiration from CLIP: CLIP demonstrated that cross-modal representations can be aligned using paired data and contrastive learning. However, joint training limits scalability to new modalities. Our method decouples the encoders, aligning their outputs via lightweight adapters.

2. Testing the Platonic Representation Hypothesis: This hypothesis suggests that models converge toward a shared statistical model of reality. Aligning diverse unimodal encoders tests whether this convergence can be explicitly achieved.

3. Scalability and Modularity: By aligning frozen encoders post hoc, our framework supports efficient integration of new modalities without the need for extensive joint training.

Related Work

Our project builds on several important advances in multimodal representation learning and theoretical insights into model convergence:

1. Platonic Representation Hypothesis (PRH): Huh et al. (2024) proposed that performant models converge toward a shared statistical model of reality in their representation spaces, regardless of their training modality. This hypothesis underpins our framework, which aims to explicitly align unimodal encoders to test this convergence hypothesis.

2. CLIP: Radford et al. (2021) introduced CLIP, a model that learns joint multimodal representations using contrastive learning on paired image-text datasets. CLIP’s success demonstrates the power of cross-modal embeddings but requires joint training of encoders, which our framework aims to circumvent.

3. Linear Mapping from Image to Text Space: Merullo et al. (2022) showed that simple linear transformations can align visual representations to text spaces, enabling cross-modal tasks like visual question answering. Their findings inspired our use of linear and lightweight MLP adapters for multimodal alignment.

4. DINOv2: Oquab et al. (2023) introduced DINOv2, a self-supervised vision transformer model that generates robust embeddings. As our performant reference model, we use DINOv2-small to provide a benchmark for evaluating the quality of our aligned multimodal representations.

5. Contrastive Representation Learning: Wang and Isola (2020) provided theoretical insights into contrastive learning by analyzing alignment and uniformity on the hypersphere. Their work shows that contrastive objectives promote both alignment of positive pairs and uniformity of representations across the hypersphere. This analysis informs our use of the dual-encoder contrastive loss to drive convergence in the shared latent space.

Hypothesis

Our work is grounded in the following hypotheses:

• A shared latent space exists where unimodal representations from different encoders can be aligned through linear transformations.
• Aligning these representations produces embeddings that closely approximate those of performant models, such as DINOv2, as measured by kernel alignment metrics.
• Multimodal alignment captures mechanisms of representation convergence, providing empirical evidence for the Platonic Representation Hypothesis.

Mathematical Framework

At the core of our project is the hypothesis that pre-trained unimodal representations can be aligned into a shared multimodal latent space. This section formalizes the mathematical structure underlying our framework, detailing how representations are extracted, aligned, and evaluated.

Multimodal Data Representation

Let the world generate raw multimodal data:

where $\mathcal{\Theta}, \mathcal{\Psi}, \mathcal{\Phi}$ represent different modalities (e.g., image, text, audio), and $\theta, \psi, \phi$ are specific instances of these modalities.

For simplicity, we focus on a two-modality setting with images ($\mathcal{X}$) and text ($\mathcal{Y}$):

Figure 2. Conceptual illustration of the connection between the Platonic Representation Hypothesis (PRH) and our project framework. Representations from different modalities (e.g., images, text) are hypothesized to converge toward a shared statistical model — the Platonic representation. Our framework uses contrastive learning to explicitly align these representations into a shared latent space, approximating this convergence.

Learned Adapters

We use frozen pre-trained encoders to extract representations:

where $d_x$ and $d_y$ are the embedding dimensions for images and text, respectively. We employ:

• ResNet-18 trained on ImageNet1K for images ($d_x = 512$).
• DistilBERT trained on BookCorpus for text ($d_y = 768$).

To project these into a shared latent space $\mathbb{R}^{d_e}$, we introduce adapters:

The adapted encoders are defined as:

where $f_\text{image}$ and $g_\text{text}$ map images and text to the shared latent space $\mathbb{R}^{d_e}$.

Dual-Encoder Contrastive Objective

To align the representations, we use a dual-encoder contrastive loss, inspired by the coursework (see Homework 4). This loss encourages positive pairs to be similar while pushing apart negative pairs:

where $\tau$ is the temperature parameter that controls the sharpness of the similarity scores.

Typically, contrastive learning applies to different “views” generated through transformations or augmentations of samples from a single modality. In our approach, we generalize this concept by treating different modalities (image and text) as distinct views of a hypothesized common underlying reality, inspired by the Platonic Representation Hypothesis.

Connection to the Platonic Representation Hypothesis

The Platonic Representation Hypothesis (PRH) posits that representations from different modalities converge toward a shared Platonic representation. In our framework, we hypothesize that contrastive alignment between the unimodal image and text encoders drives this convergence.

Our aligned multimodal encoder is defined as:

where $\lambda$ is a learnable parameter controlling the balance between the two modalities.

Performant Model Benchmark

To evaluate the quality of our aligned multimodal representations, we use the DINOv2-small encoder as a benchmark. Specifically, we define the function implemented by the DINOv2-small feature extractor as:

The DINOv2 encoder serves as a performant reference model, providing high-quality image representations. By comparing our aligned multimodal representations to the DINOv2 representations, we measure how effectively our contrastive alignment approximates this benchmark.

Kernel Alignment Metric

We characterize representations in terms of their kernels, which capture the similarity between data points. Two representations are considered aligned if their kernels are similar for corresponding inputs. Given the kernels:

• $K_X(i, j) = \langle f_{\text{image}}(x^{(i)}), f_{\text{image}}(x^{(j)}) \rangle$
• $K_Y(i, j) = \langle g_{\text{text}}(y^{(i)}), g_{\text{text}}(y^{(j)}) \rangle$
• $K_{\text{align}}(i, j) = \langle h_\text{multi}(x^{(i)}, y^{(i)}), h_\text{multi}(x^{(j)}, y^{(j)}) \rangle$
• $K_{\text{DINOv2}}(i, j) = \langle \text{DINOv2}(x^{(i)}), \text{DINOv2}(x^{(j)}) \rangle$

we evaluate alignment performance using the mutual-KNN kernel alignment metric $m$.

Specifically, we compute the following values:

Unimodal Alignment:

• $m(K_X, K_{\text{DINOv2}})$: Alignment of the image encoder $f_\text{image}$ kernel with the DINOv2 kernel.
• $m(K_Y, K_{\text{DINOv2}})$: Alignment of the text encoder $g_\text{text}$ kernel with the DINOv2 kernel.

Multimodal Alignment:

• $m(K_{\text{align}}, K_{\text{DINOv2}})$: Alignment of the multimodal encoder $h_\text{multi}$ kernel with the DINOv2 kernel.

We conjecture that the aligned multimodal kernel will have higher similarity with $K_{\text{DINOv2}}$ than the unimodal kernels.

Methodology

All code for this project is available in our GitHub Repository.

Data Pipeline

We use the first 12,800 samples of the Flickr30k dataset, which contains paired image-caption samples. Each image is paired with the first caption, forming a single positive pair $(x^{(i)}, y^{(i)})$.

Image Processing:

• Resize to 224x224.
• Normalize using ImageNet statistics.
• Convert to tensors for ResNet-18.

Text Processing:

• Tokenize with DistilBERT tokenizer.
• Pad/truncate to 64 tokens.
• Convert to tensors for DistilBERT.

Data Loading:

• Batch size: 256.
• Train-validation split: 75%-25%.

Model Architecture

We use frozen pre-trained encoders with trainable adapters to align representations in a shared multimodal space:

Frozen Encoders:

• Image Encoder: ResNet-18 ($d_x = 512$).
• Text Encoder: DistilBERT ($d_y = 768$).

Adapters:

• Linear Adapter: Matrix multiplication by $W_x$ or $W_y$ plus bias term.
• MLP Adapter: 2-layer MLP with GELU and LayerNorm.

Reference Model: DINOv2-small ($d_e = 768$).

Training Procedure

We train the adapters using the dual-encoder contrastive loss for 100 epochs on Flickr30k with a temperature parameter $\tau = 0.02$ in the contrastive loss. Other relevant hyperparameter settings:

• Optimizer: AdamW
• Learning Rate: $1 \times 10^{-4}$ (cosine decay with warmup).
• Gradient Clipping: 0.5.
• Weight Decay: 0.001 (linear adapter) and 0.005 (MLP adapter).
• Label Smoothing: 0.05.
• Dropout: 0.1.

Evaluation Metrics

We will test two key hypotheses based on the mutual-kNN values we described in the Mathematical Framework, before and after training:

• Weak Hypothesis ($H_1$): The aligned multimodal kernel achieves higher similarity with the DINOv2 kernel than the average of the unimodal kernels: \(m(K_{\text{align}}, K_{\text{DINOv2}}) > \text{avg}(m(K_X, K_{\text{DINOv2}}), m(K_Y, K_{\text{DINOv2}})).\)

• Strong Hypothesis ($H_2$): The aligned multimodal kernel surpasses even the best unimodal kernel: \(m(K_{\text{align}}, K_{\text{DINOv2}}) > \max(m(K_X, K_{\text{DINOv2}}), m(K_Y, K_{\text{DINOv2}})).\)

Results

Kernel Alignment Improves with Training

Our first key finding is that the mutual-KNN kernel alignment metric improves after training for both the linear and MLP adapters. This demonstrates that our contrastive alignment objective effectively aligns the image and text representations.

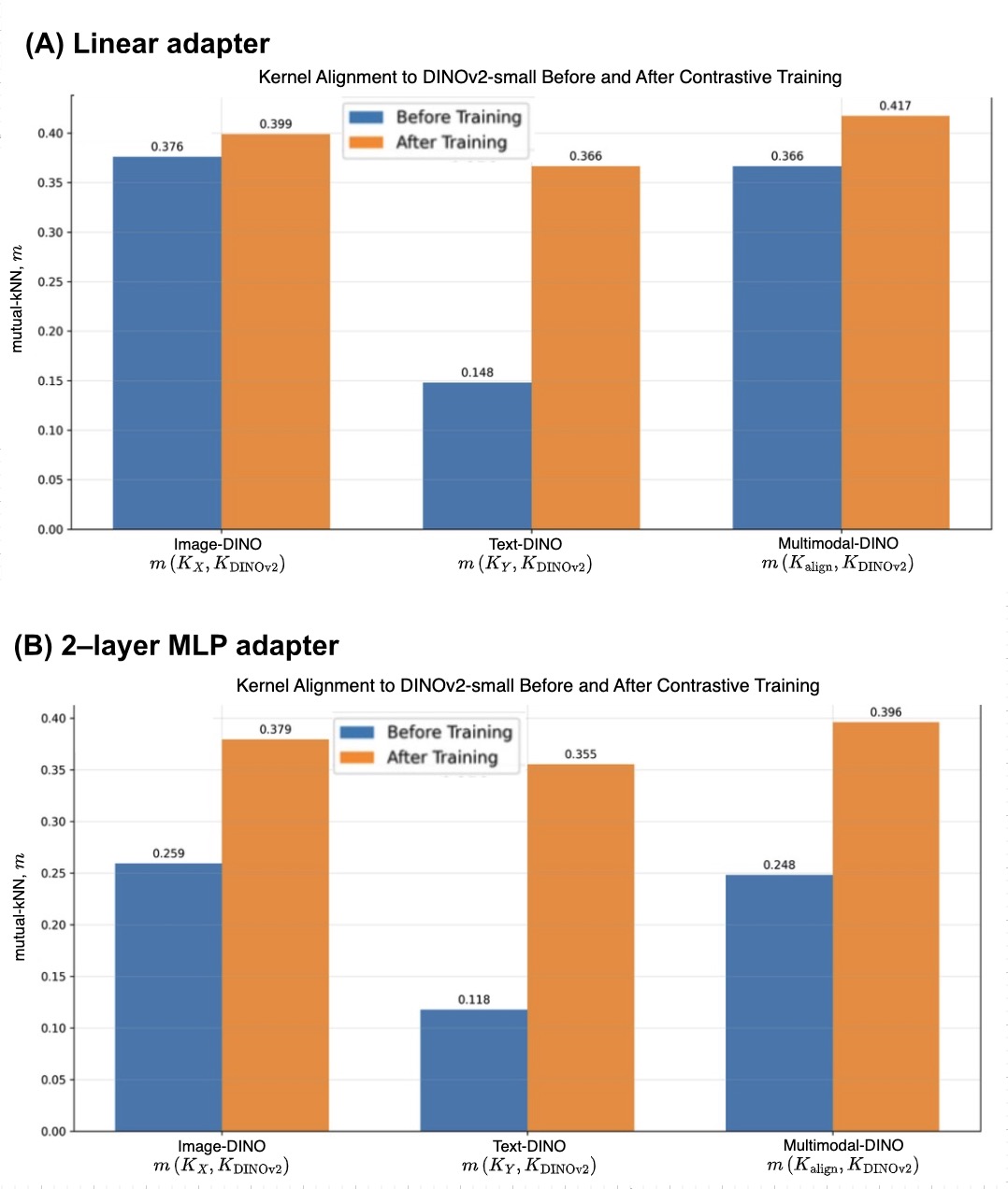Figure 3. Bar plot showing the mutual-KNN kernel alignment metric before and after training for the (A) linear and (B) 2-layer MLP adapters. For both adapter types and all encoders, kernel alignment to the DINOv2-small encoder improves after training with the dual-encoder contrastive objective.

We observe that prior to training, the alignment scores are relatively low, particularly for the text encoder. After training, there is a significant increase in alignment for both the image and text encoders. The multimodal alignment scores exceed the individual unimodal scores, suggesting that the adapters successfully bridge the gap between the modalities.

Visualization of Alignment

To further illustrate the alignment process, we apply dimensionality reduction to visualize the embeddings produced by the DINOv2-small encoder and our aligned multimodal encoder. To explain using principal component analysis (PCA), we compute the principal components (PCs) of the DINOv2-small embeddings and project the multimodal embeddings onto the same PCs. Multidimensional scaling (MDS) is a similar technique but nonlinear.

The visualization shows that during training, the aligned multimodal embeddings progressively move closer to the DINOv2 embeddings, supporting the hypothesis that our contrastive objective aligns the representations effectively.

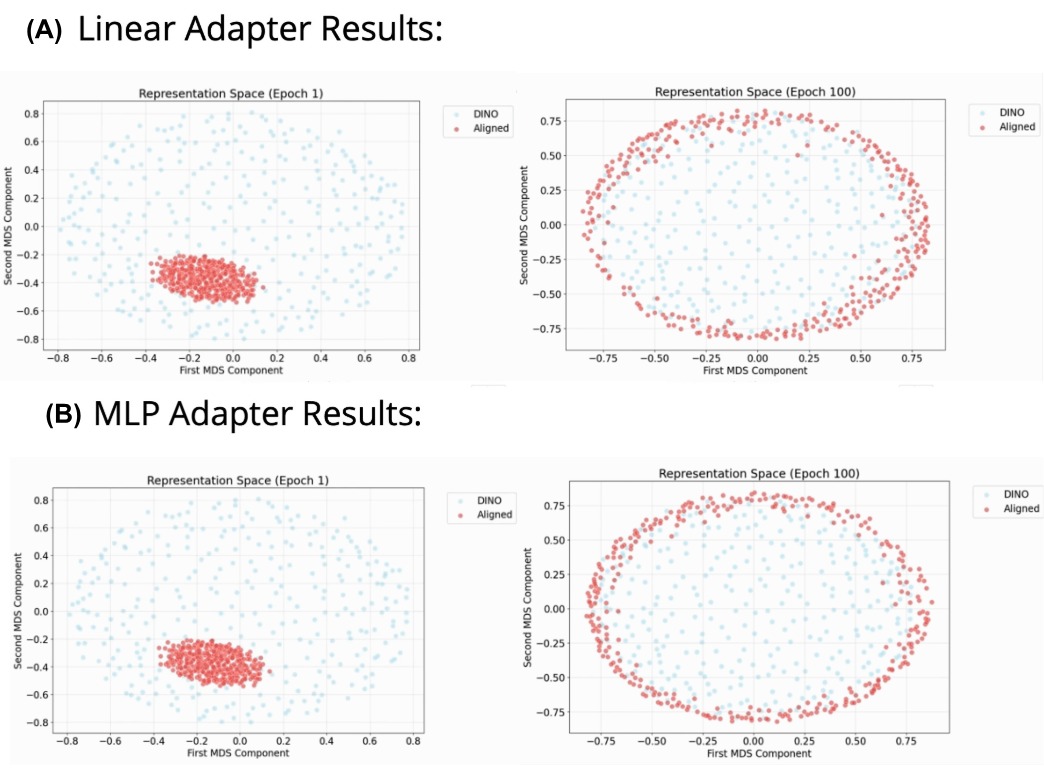Figure 4. MDS plots of the embeddings from the DINOv2-small encoder (blue) and our aligned multimodal encoder (yellow) at the first epoch (left) and last epoch (right) of training, for both types of adapters: (A) linear and (B) MLP adapters. The multimodal representations become progressively more aligned with the DINOv2 embeddings during training.

Key Hypotheses Supported

Our results validate both the weak hypothesis ($H_1$) and the strong hypothesis ($H_2$). Specifically:

• Weak Hypothesis ($H_1$): The aligned multimodal kernel achieves higher similarity with the DINOv2 kernel than the average of the unimodal kernels.
• Strong Hypothesis ($H_2$): The aligned multimodal kernel surpasses even the best unimodal kernel.

This indicates that the multimodal representations, which incorporate both image and text information, are more closely aligned with the DINOv2 embeddings than either the image or text representations alone.

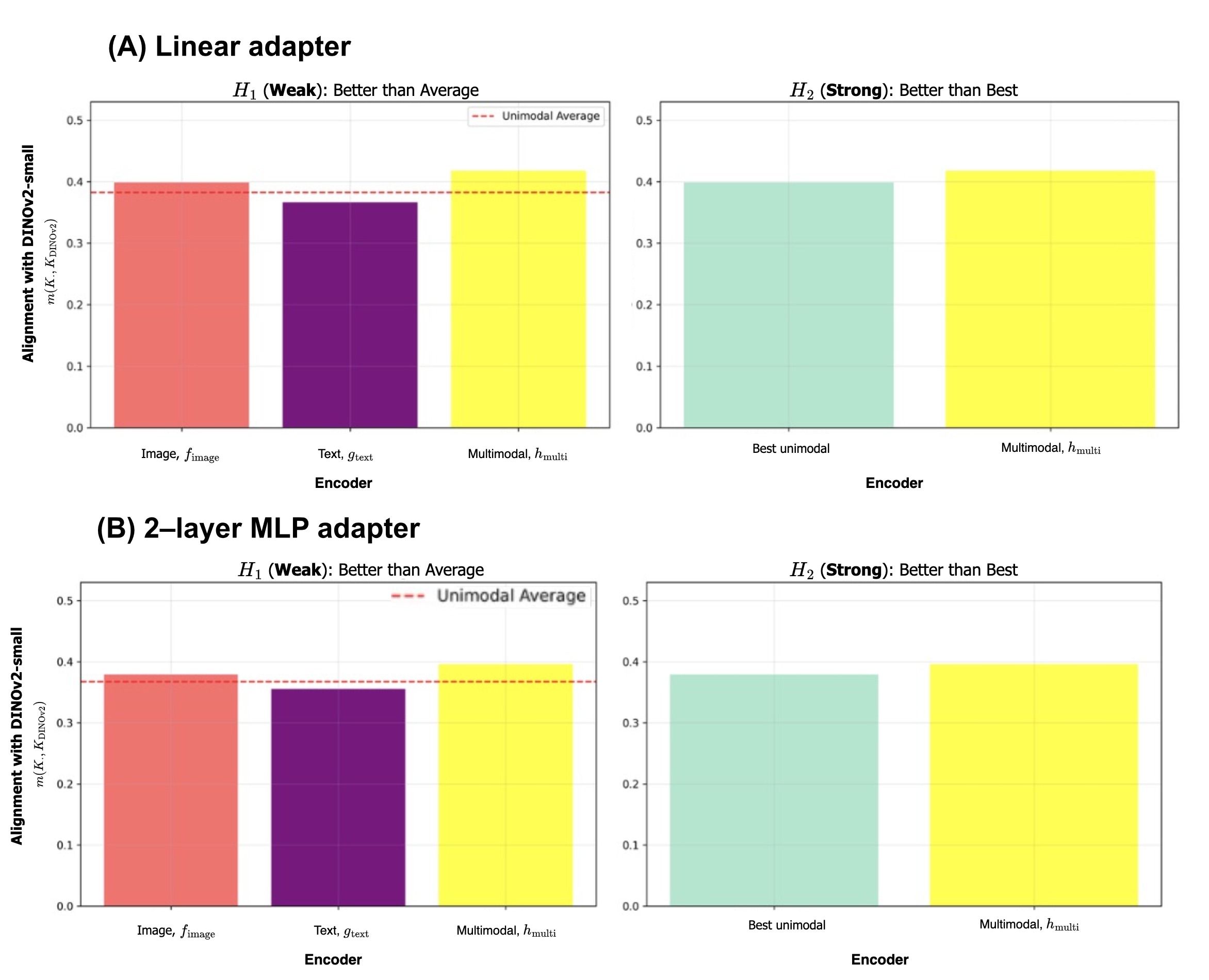Figure 5. The mutual-KNN kernel alignment metric for our aligned multimodal encoder surpasses both the (left) average of and the (right) better of the two unimodal encoders, supporting both the weak and strong hypotheses. Results are shown for both (A) linear adapters and (B) 2-layer MLP adapters.

Notably, the multimodal alignment scores consistently exceed the individual image and text alignment scores, indicating an emergent property where the whole (multimodal representation) is greater than the sum of its parts (unimodal representations). This finding is particularly compelling given that the DINOv2 model is a vision-only model trained without any text supervision.

Our results suggest that incorporating multimodal information enhances the quality of the learned representations, supporting the Platonic Representation Hypothesis. This hypothesis posits a shared statistical model of reality underlying different modalities. The fact that multimodal alignment produces representations closer to DINOv2 — a high-performing vision model — reinforces the idea that such a shared model exists.

In summary, our findings demonstrate that aligning image and text representations using simple linear or MLP adapters can produce embeddings that not only match but exceed the performance of unimodal representations when compared to a performant model like DINOv2.

Discussion

In this work, we investigated whether representations from pre-trained unimodal encoders can be aligned into a shared multimodal latent space using lightweight adapters. Our results support the Platonic Representation Hypothesis (PRH) proposed by Huh et al. (2024). Specifically, we observed that aligning image and text embeddings via contrastive learning produces multimodal representations more closely aligned with DINOv2-small features compared to unimodal representations alone.

Inspired by the CLIP framework (Radford et al., 2021), which aligns cross-modal representations through joint training, our approach achieves alignment post hoc using frozen encoders and lightweight adapters. This offers a scalable alternative to joint training for multimodal learning.

Key Insights

• Cross-Modal Alignment: Despite DINOv2-small being a self-supervised vision model trained without text supervision, aligning image and text representations improved their similarity to DINOv2 embeddings. This suggests a universal structure in representation spaces, reinforcing the PRH’s concept of convergence toward a shared statistical model of reality.

• Generalized Contrastive Views: Our dual-encoder contrastive objective extends the traditional notion of “views” in contrastive learning to distinct modalities, treating them as different perspectives of an underlying reality. This insight differentiates our work from conventional contrastive learning.

• Empirical Hypothesis Validation: Our findings validate both the weak and strong hypotheses, demonstrating that multimodal alignment yields representations that outperform unimodal representations when compared to DINOv2 embeddings.

Non-Trivial Alignment to DINOv2

Importantly, our multimodal encoder was not explicitly optimized to match DINOv2-small embeddings. The fact that the aligned encoder $h_{\text{multi}}(x, y)$ produces representations closer to DINOv2 compared to the image encoder alone indicates a genuine benefit of multimodal alignment, rather than mere replication of image features.

Potential Limitations

• Dataset Bias: The Flickr30k dataset primarily features images of people in everyday situations. This limited diversity may affect the generalizability of our findings. Exploring more diverse datasets could offer further insights.

• Restricted Modalities: Our study focused on image and text alignment. Extending the framework to additional modalities, such as audio or video, could provide a broader validation of the alignment mechanism and PRH.

Conclusion

Our work demonstrates that multimodal alignment via contrastive learning is a promising approach for achieving efficient, scalable representation learning. The observed convergence toward DINOv2 embeddings supports the notion of a universal Platonic representation, where aligning multiple modalities reveals shared underlying structures in representation spaces. This result builds upon insights from both the CLIP framework and the Platonic Representation Hypothesis, underscoring the potential of multimodal alignment in advancing our understanding of representation learning.

Future Directions

1. Leveraging Multiple Captions for Alignment

In this work, we used only the first caption from the Flickr30k dataset per image. To improve alignment, we plan to use all five captions per image. Each data point $i$ will be represented as $(x^{(i)}, y_1^{(i)}, \dots, y_5^{(i)})$, where $y_k^{(i)}$ is the $k$-th caption. The contrastive loss becomes:

2. Scaling to Richer Multimodal Datasets

We aim to extend our experiments to include a third modality, such as audio. For example, using the VGGSound dataset and a pre-trained audio encoder like Wav2Vec, we can evaluate whether adding audio improves alignment compared to the image-text setting.

We will also generalize the dual-encoder loss to a multi-encoder contrastive loss for $M$ modalities:

3. Zero-Shot Evaluation with Pre-Trained Heads

We plan to evaluate the quality of our aligned representations using pre-trained classifier heads from the DINOv2 GitHub repository. Specifically, we will replace the DINOv2-small encoder with our aligned multimodal encoder $h_\text{multi}$ and test zero-shot classification performance on ImageNet.